VOIE GÉNÉRALE
ENSEIGNEMENT DE SPÉCIALITÉ
Mathématiques
Présentation
L’enseignement de spécialité de mathématiques permet aux élèves de renforcer et d’approfondir l’étude des thèmes suivants : « Algèbre », « Analyse », « Géométrie », « Probabilités et statistique » et « Algorithmique et programmation ». Cet enseignement s’ouvre à l’histoire des mathématiques pour expliquer l’émergence et l’évolution des notions et permet aux élèves d’accéder à l’abstraction et de consolider la maîtrise du calcul algébrique. L’utilisation de logiciels, d’outils de représentation, de simulation et de programmation favorise l’expérimentation et la mise en situation. Les interactions avec d’autres enseignements de spécialité tels que physique-chimie, sciences de la vie et de la Terre, sciences de l’ingénieur, sciences économiques et sociales sont valorisées.
Principes et objectifs
La classe de première générale est conçue pour préparer au baccalauréat général, et au-delà à une poursuite d’études réussie et à l’insertion professionnelle.
L’enseignement de spécialité de mathématiques de la classe de première générale est conçu à partir des intentions suivantes :
-
- permettre à chaque élève de consolider les acquis de la seconde, de développer son goût des mathématiques, d’en apprécier les démarches et les objets afin qu’il puisse faire l’expérience personnelle de l’efficacité des concepts mathématiques et de la simplification et la généralisation que permet la maîtrise de l’abstraction
-
- développer des interactions avec d’autres enseignements de spécialité
- préparer au choix des enseignements de la classe de terminale, notamment choix de l’enseignement de spécialité de mathématiques
Les thématiques de la spécialité
Le programme s’organise en cinq grandes parties :
- Algèbre
- Analyse
- Géométrie
- Probabilités et statistiques
- Algorithmique et programmation
La diversité des activités mathématiques proposées permet aux élèves de prendre conscience de la richesse et de la variété de la démarche mathématique et de la situer au sein de l’activité scientifique. Cette prise de conscience est un élément essentiel dans la définition de leur orientation.
Les étapes de verbalisation et de reformulation jouent un rôle majeur dans l’appropriation des notions mathématiques et la résolution des problèmes.
Une spécialité qui prépare à la réussite
Comme toutes les disciplines, les mathématiques contribuent au développement des compétences orales à travers notamment la pratique de l’argumentation. Celle-ci conduit à préciser sa pensée et à expliciter son raisonnement de manière à convaincre. Elle permet à chacun de faire évoluer sa pensée, jusqu’à la remettre en cause si nécessaire, pour accéder progressivement à la vérité par la preuve.
Des situations variées se prêtent à la pratique de l’oral en mathématiques : la reformulation par l’élève d’un énoncé ou d’une démarche, les échanges interactifs lors de la construction du cours, les mises en commun après un temps de recherche, les corrections d’exercices, les travaux de groupe, les exposés individuels ou à plusieurs… L’oral mathématique mobilise à la fois le langage naturel et le langage symbolique dans ses différents registres (graphiques, formules, calcul).
Compétences travaillées et méthodes acquises
Dans le prolongement des cycles précédents, la spécialité mathématiques travaille les six grandes compétences :
-
- chercher, expérimenter, en particulier à l’aide d’outils logiciels
- modéliser, faire une simulation, valider ou invalider un modèle
- représenter, choisir un cadre (numérique, algébrique, géométrique…), changer de registre
- raisonner, démontrer, trouver des résultats partiels et les mettre en perspective
- calculer, appliquer des techniques et mettre en œuvre des algorithmes
- communiquer un résultat par oral ou par écrit, expliquer une démarche.
La résolution de problèmes est un cadre privilégié pour développer, mobiliser et combiner plusieurs de ces compétences. Cependant, pour prendre des initiatives, imaginer des pistes de solution et s’y engager sans s’égarer, l’élève doit disposer d’automatismes. Ceux-ci facilitent en effet le travail intellectuel en libérant l’esprit des soucis de mise en œuvre technique et élargissent le champ des démarches susceptibles d’être engagées.
L’installation de ces réflexes est favorisée par la mise en place d’activités notamment de calcul (mental ou réfléchi, numérique ou littéral). Elle est menée conjointement avec la résolution de problèmes, afin de stabiliser connaissances, méthodes et stratégies.
L’utilisation de logiciels (calculatrice ou ordinateur), d’outils de visualisation et de représentation, de calcul, de simulation, de programmation développe la possibilité d’expérimenter, favorise l’interaction entre l’observation et la démonstration et change profondément la nature de l’enseignement des mathématiques.
Informations extraites du Bulletin Officiel de l’Education Nationale
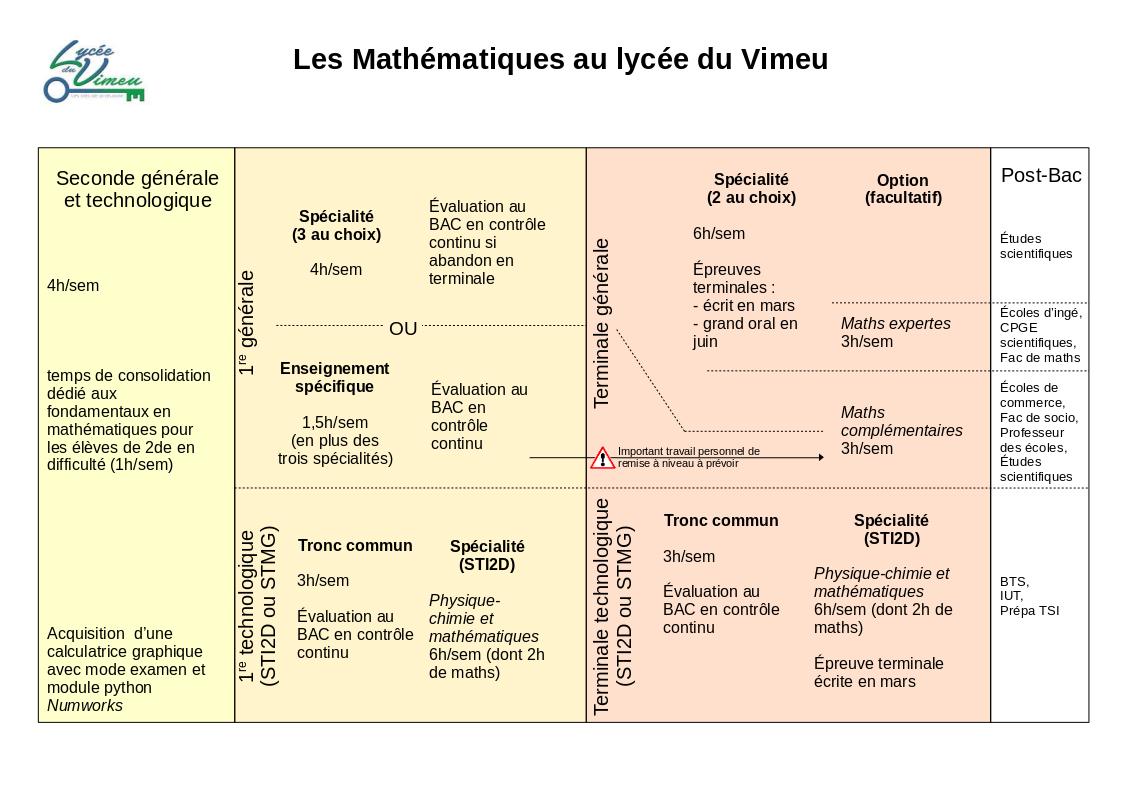
Les mathématiques au Lycée du Vimeu